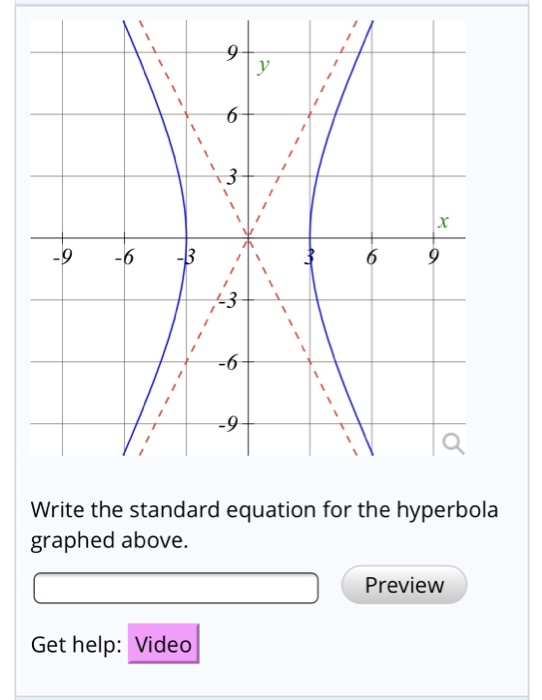
Math Algebra Algebra questions and answers Write the standard equation for the hyperbola graphed above. Write the standard equation for the hyperbola graphed above. This problem has been solved! You’ll get a detailed solution from a subject matter expert that helps you learn core concepts. See Answer
If the transverse axis of a hyperbola is 12 and the eccentricity is 4/3, then what is the equation of this hyperbolas center, verex, foci, asymptotes and sketch the graph? – Quora
These points are what controls the entire shape of the hyperbola since the hyperbola’s graph is made up of all points, P, such that the distance between P and the two foci are equal. To determine the foci you can use the formula: a 2 + b 2 = c 2. transverse axis: this is the axis on which the two foci are. asymptotes: the two lines that the
Source Image: chegg.com
Download Image
In analytic geometry, a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other (Figure 10.2.2 ). Figure 10.2.2: A hyperbola.
Source Image: openalgebra.com
Download Image
Solved y 6 3 20 -6 . Q Write the standard equation for the | Chegg.com Write equations of hyperbolas in standard form. Graph hyperbolas centered at the origin. Graph hyperbolas not centered at the origin. Solve applied problems involving hyperbolas. What do paths of comets, supersonic booms, ancient Grecian pillars, and natural draft cooling towers have in common? They can all be modeled by the same type of conic.
Source Image: chegg.com
Download Image
Write The Standard Equation For The Hyperbola Graphed Above
Write equations of hyperbolas in standard form. Graph hyperbolas centered at the origin. Graph hyperbolas not centered at the origin. Solve applied problems involving hyperbolas. What do paths of comets, supersonic booms, ancient Grecian pillars, and natural draft cooling towers have in common? They can all be modeled by the same type of conic. Let us check through a few important terms relating to the different parameters of a hyperbola. Foci of hyperbola: The hyperbola has two foci and their coordinates are F(c, o), and F'(-c, 0). Center of Hyperbola: The midpoint of the line joining the two foci is called the center of the hyperbola. Major Axis: The length of the major axis of the hyperbola is 2a units.
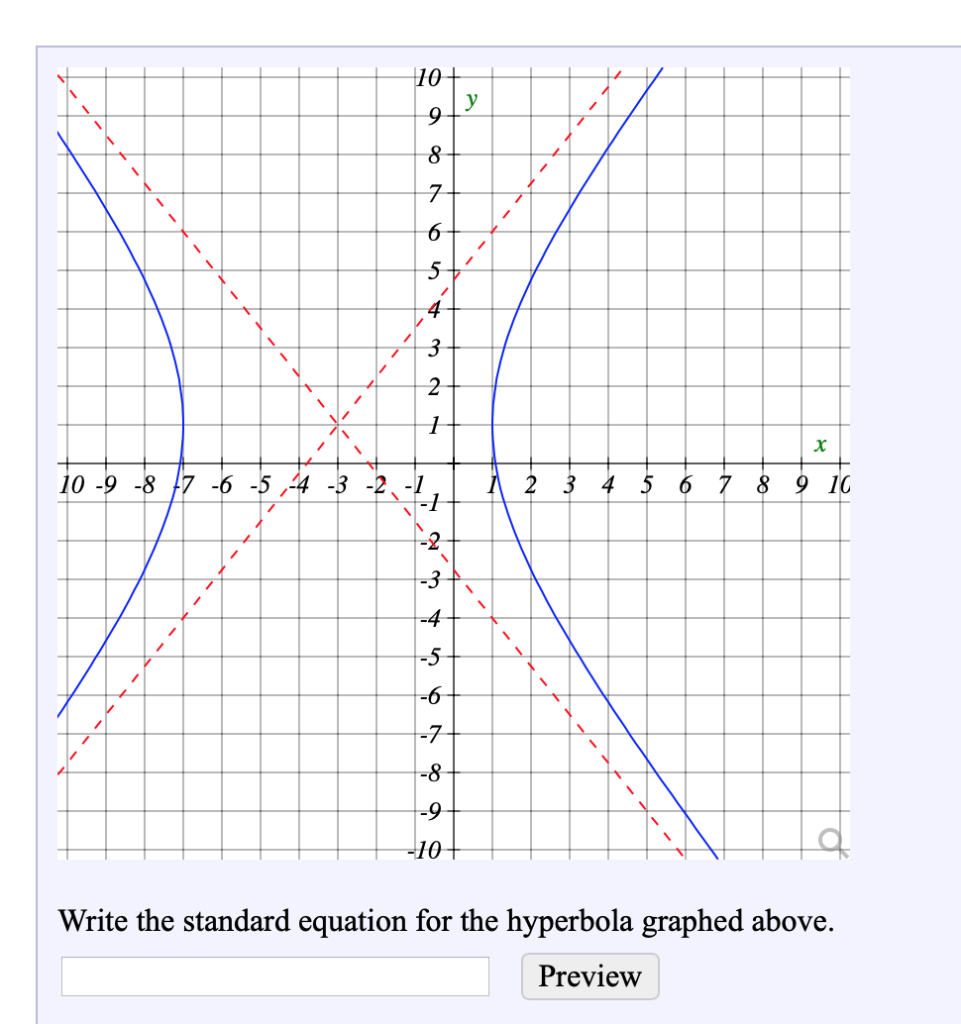
Solved 10+ 8 7 5 4 3 2 9 10 -8 7 -6 -5 4 -3 -2. -1 1 2 10 -9 | Chegg.com
The standard form of the equation of a hyperbola with center (0,0) ( 0, 0) and transverse axis on the x -axis is. x2 a2 − y2 b2 =1 x 2 a 2 − y 2 b 2 = 1. where. the length of the transverse axis is 2a 2 a. the coordinates of the vertices are (±a,0) ( ± a, 0) the length of the conjugate axis is 2b 2 b. PPT – 4 th EDITION PowerPoint Presentation, free download – ID:1785585

Source Image: slideserve.com
Download Image
IXL – Write equations of hyperbolas in standard form using properties (Algebra 2 practice) The standard form of the equation of a hyperbola with center (0,0) ( 0, 0) and transverse axis on the x -axis is. x2 a2 − y2 b2 =1 x 2 a 2 − y 2 b 2 = 1. where. the length of the transverse axis is 2a 2 a. the coordinates of the vertices are (±a,0) ( ± a, 0) the length of the conjugate axis is 2b 2 b.

Source Image: ixl.com
Download Image
If the transverse axis of a hyperbola is 12 and the eccentricity is 4/3, then what is the equation of this hyperbolas center, verex, foci, asymptotes and sketch the graph? – Quora Math Algebra Algebra questions and answers Write the standard equation for the hyperbola graphed above. Write the standard equation for the hyperbola graphed above. This problem has been solved! You’ll get a detailed solution from a subject matter expert that helps you learn core concepts. See Answer
Source Image: quora.com
Download Image
Solved y 6 3 20 -6 . Q Write the standard equation for the | Chegg.com In analytic geometry, a hyperbola is a conic section formed by intersecting a right circular cone with a plane at an angle such that both halves of the cone are intersected. This intersection produces two separate unbounded curves that are mirror images of each other (Figure 10.2.2 ). Figure 10.2.2: A hyperbola.
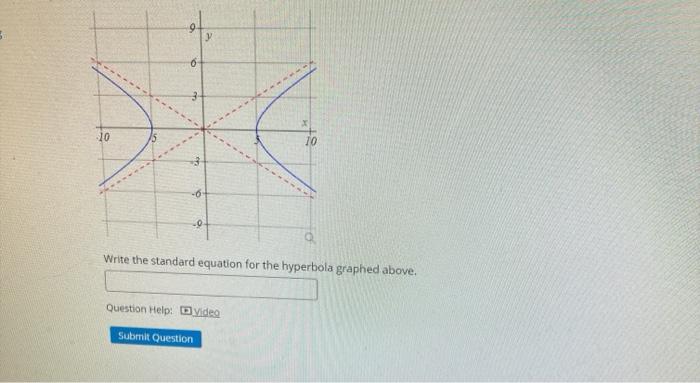
Source Image: chegg.com
Download Image
Write an equation for the hyperbola shown in the graph. | Homework.Study.com Free Hyperbola calculator – Calculate Hyperbola center, axis, foci, vertices, eccentricity and asymptotes step-by-step

Source Image: homework.study.com
Download Image
Answered: Which equation represents the hyperbola… | bartleby Write equations of hyperbolas in standard form. Graph hyperbolas centered at the origin. Graph hyperbolas not centered at the origin. Solve applied problems involving hyperbolas. What do paths of comets, supersonic booms, ancient Grecian pillars, and natural draft cooling towers have in common? They can all be modeled by the same type of conic.
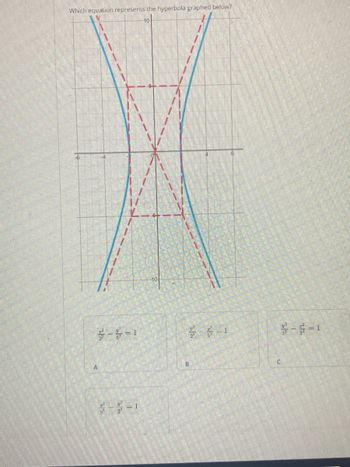
Source Image: bartleby.com
Download Image
Algebra – Hyperbolas Let us check through a few important terms relating to the different parameters of a hyperbola. Foci of hyperbola: The hyperbola has two foci and their coordinates are F(c, o), and F'(-c, 0). Center of Hyperbola: The midpoint of the line joining the two foci is called the center of the hyperbola. Major Axis: The length of the major axis of the hyperbola is 2a units.
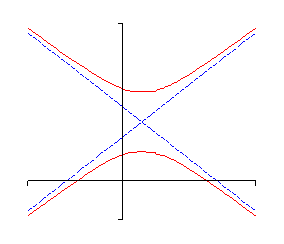
Source Image: tutorial.math.lamar.edu
Download Image
IXL – Write equations of hyperbolas in standard form using properties (Algebra 2 practice)
Algebra – Hyperbolas These points are what controls the entire shape of the hyperbola since the hyperbola’s graph is made up of all points, P, such that the distance between P and the two foci are equal. To determine the foci you can use the formula: a 2 + b 2 = c 2. transverse axis: this is the axis on which the two foci are. asymptotes: the two lines that the
Solved y 6 3 20 -6 . Q Write the standard equation for the | Chegg.com Answered: Which equation represents the hyperbola… | bartleby Free Hyperbola calculator – Calculate Hyperbola center, axis, foci, vertices, eccentricity and asymptotes step-by-step